Standardthemen in moderner Sicht: Was bedeutet das für den
Geometrie-Unterricht? Nun, auch in moderner Sicht bleibt die Innenwinkelsumme im
Dreieck 180° und bleibt die Formel für den Flächeninhalt eines Dreiecks.
Moderne Sicht heißt: moderne Werkzeuge, moderne Methoden.
Zunächst eine kurze Rückschau.
Die Geometrie der Antike
basierte auf Konstruktionen mit Zirkel und Lineal (ohne Längenskala). Objekte
waren zunächst: Punkte, Strecke/Strahl/Gerade, Dreiecke/Polygone, Kreis, ... .
Erst später kamen Zahlen hinzu: Längen, Winkel, Flächeninhalte, ... . Als
Werkzeug wurde das Lineal um eine Längenskala erweitert und später der
Winkelmesser entwickelt. Das Geodreieck beinhaltete schließlich neben Längen
und Winkeln auch Parallele und Senkrechte (frühe Makros!) und ist mittlerweile
unstrittiges Werkzeug des Geometrie-Unterrichts.
Mit der zunehmenden
Verbreitung von Computern gab es in den 80er Jahren Geometriesoftware der 1.
Generation, mit der man wie mit Zirkel und Lineal konstruieren konnte (z. B.
KOBESCH). Diese brachte aber keine wesentlichen Impulse und didaktischen
Neuerungen und konnte sich nicht durchsetzen.
Neue Impulse sowohl inhaltlicher als auch
methodischer Art kamen erst durch die Dynamische
Geometrie-Software (DGS) wie z. B. Cabri, Euklid, Geolog.
Zugmodus, Makros und Ortslinien sind die typischen Eigenschaften. Sie ermöglichten
experimentelles Arbeiten, visuelles Argumentieren sowie heuristische Strategien.
Inhaltlich gab es einerseits neue Themenbereiche (z. B. Euler-Gerade, Ortslinien,
Kreisinversion), die vorher nicht zugänglich waren, andererseits kam man oft
wieder zu klassischen Konstruktionen und Problemen zurück.
Der unterrichtliche
Einsatz ist aber nicht ohne Tücken:
·
Zunächst braucht man einen freien
Computerraum mit genügend Arbeitsplätzen.
·
Dann ist in der Regel eine längere
Durststrecke von Konstruktionen zu überwinden, bevor mathematisch Aktivitäten
anhand der konstruierten Figuren stattfinden können.
·
Es passiert häufig, dass etliche Schülergruppen
nicht fertig werden.
·
Ständig kommt es auch vor, dass durch Fehler
in der Konstruktion Figuren entstehen, die nicht das leisten, was sie sollen und
deshalb für den weiteren mathematischen Unterrichtsgang ungeeignet sind!
Neben der Angst vor
solchen Fallen in der Durchführung gibt es bei vielen Lehrern auch grundsätzliche
Vorbehalte, z. B. dass die Schüler den Umgang mit Zeichengeräten ganz
verlernen oder dass die im Zugmodus erlebte Evidenz das Beweisbedürfnis weiter
vermindert.
Auch muss zu den sowieso vorhandenen
Anforderungen an geometrische Konstruktionen (oder Beweisführungen) jetzt noch
ein Wissen über die Bedienung von DGS und deren Objekt-Philosophie
(Unterscheidung in freie Punkte/ gebundene Punkte/ Schnittpunkte, Konzept der
Freiheitsgrade, Hierarchien von Objekten) hinzukommen, um erfolgreich tätig zu
sein.
All das führte
dazu, dass zwar auf der theoretischen Ebene der Hochschul-Didaktik die
Auswirkungen der DGS auf die Konzeption von Geometrie-Unterricht beachtlich
waren, im real existierenden Unterricht es aber bei vereinzelten Aktionen von überzeugten
Enthusiasten blieb.
Das Konstruieren geometrischer Figuren mit DGS erwies sich letzten Endes
als eine spezielle Form des Programmierens, sei es als mausgesteuertes
Programmieren auf einer graphischen Benutzeroberfläche, sei es als
tastaturgesteuerte Eingabe von Konstruktionsbefehlen im Sinne eines
Konstruktionsprogramms. Dies geometrische Programmieren in einer Klasse 7-8-9
war zeitaufwendig und fehleranfällig und stellte an Lehrer und Schüler hohe
Anforderungen.
Hier setzt nun die Idee elektronischer Arbeitsblätter an:
Weg vom Programmieren als Konstruieren von Figuren ist die Devise, hin zum Arbeiten mit geometrischen Figuren, zum Experimentieren, zum Deuten von
Ortslinien, zum Aufstellen und Überprüfen von Vermutungen, zum Entdecken von
Eigenschaften, in der Folge auch zum Herstellen von Querverbindungen und Begründungszusammenhängen.
Solche elektronischen Arbeitsblätter enthalten vorbereitete
Konstruktionen und integrierte Aufgabentexte. Sie verstehen sich als eine
mediale Brücke zwischen der Welt der Mathematik (den geometrischen Sätzen) und
der Welt der DGS (mit ihrer Objektphilosophie, ihren Konstruktionsbefehlen, dem
Zugmodus und den Ortslinien), sie können ohne vertiefte Kenntnis des jeweiligen
Programms eingesetzt werden.
Jeder Schüler ist
aktiv tätig statt passiv zuhörend. Durch ein interaktives Werkzeug wird
individuelles und selbstgesteuertes Lernen möglich; Experimentieren, Vermuten
und Überprüfen wird selbstverständlicher Teil des Lernprozesses.
Mit solchen elektronischen Arbeitsblättern wandelt sich die Rolle des Schülers.
Vom Objekt der Belehrung wird er mehr zum Subjekt eigenen Lernens. Die Zulassung
und Betonung des Visuellen und die Aufforderung zum experimentellen Arbeiten
geben dem Geometrie-Unterricht einen anderen Charakter und erhöhen die Möglichkeiten
zum selbstständigen Arbeiten.
Akzeptiert man den
derzeitigen Stand der Lernpsychologie, so konstruiert sich jeder Schüler auf
der Basis seiner Vorerfahrungen sein eigenes Wissen (Subjektive
ErfahrungsBereiche im
Sinne von Bauersfeld). Besteht schon im klassischen lehrerzentrierten die Gefahr
eines Flickenteppichs aus unterschiedlichem Wissen, so kann es bei
elektronischen Arbeitsblättern, die auf ein hohes Maß an Eigentätigkeit der
Schüler abzielen, noch eher passieren, lauter isolierte Wissensinseln zu
produzieren. Die neue Rolle des Lehrers wird deshalb darin bestehen, die im
Einzelnen aufgebauten subjektiven Erfahrungen und Deutungen der Schüler zu
sammeln, ggfs. zu korrigieren, zu organisieren und vernetzen und eine gemeinsame
Wissensbasis für zukünftiges Arbeiten herzustellen. Dabei ist es wichtig,
verschiedene Lösungswege einzubeziehen und auch auf unfertige oder fehlerhafte
Ansätze einzugehen.
Der Lehrer ist in
der Zeit, in der die Schüler an den Arbeitsblättern arbeiten, nicht
arbeitslos. Seine gewandelte Aufgabe besteht darin, herumzugehen und den
Arbeitsprozess der Schüler zu beobachten und sich innerlich Notizen zu machen
über Aspekte, die in der Auswertung angesprochen werden sollen. Falls
erforderlich gibt er einzelnen Gruppen Hinweise (notfalls auch zentral) oder
besonders schnellen Schülern Zusatzaufgaben.
Entdeckendes Arbeiten braucht Zeit und Ruhe, eine Wettkampfmentalität ist da
eher hinderlich.
Die Arbeit am
Computer ist nur ein Teil der Schüleraktivität. Eine Dokumentation gehört
untrennbar dazu und ist wesentliche Voraussetzung für die abschließende
Besprechung. Für eine solche Dokumentation sind mehrere Formen denkbar: eine
Notiz im Heft oder elektronisch in Textboxen oder Word-Texte, ein Ausdruck der Lösungsfigur
oder eine Zeichnung mit Zirkel und Lineal oder eine einfache Handskizze. Für
die Auswertung und Besprechung ist genügend Zeit vorzusehen.
Dabei wird auch ein
anderer Umgang mit Fehlern erforderlich. Zum visuellen und experimentellen
Arbeiten gehört das Aufstellen von Vermutungen. „Falsche“ Vermutungen
kommen dabei häufig vor und sind nicht als Fehler zu bewerten, sondern als
Stufen im Erkenntnisprozess und als Chance im Lernprozess. Dafür ist
wesentlich, dass die Schüler in einer Lernumgebung arbeiten, die zum Vermuten
und Ausprobieren ermutigt. Das in Deutschland vorherrschende
fragend-entwickelnde Lehrer-Schüler-Unterrichtsgespräch erweist sich als
Unterrichtsmethode eher hinderlich, weil es zum einen sehr stark den Denkprozess
in Richtung der vor Lehrer vorgedachten Lösung einengt und weil es
unausgesprochen Lernsituation und Leistungsfeststellung verquickt.
Experimentelles oder anschauliches Arbeiten
hat keine Tradition im Geometrie-Unterricht. Seit mehr als 2000 Jahren ist unser
Geometrie-Verständnis durch das Werk Euklids geprägt. Auf Axiomen aufbauend
gibt es ein Gebäude von Lehrsätzen, die durch logische Deduktionen aus den
Axiomen oder schon bewiesenen Sätzen hergeleitet werden, ohne auf die
Anschauung zurückzugreifen.
Dies ist aber nicht der Weg, wie Erkenntnis
entsteht und sich individuell Wissen aufbaut! Der Geometrie-Unterricht war mehr
wissenschaftstheoretisch als lernpsychologisch und erkenntnistheoretisch
konzipiert. Das Aufkommen der Abbildungsgeometrie verstärkte die Problematik,
weil zur verfrühten Formalisierung noch eine Algebraisierung der Geometrie
hinzukam.
Auf die Problematik, in der Sekundarstufe I Beweise(n) in strenger formaler
Weise zu unterrichten, wurde von Didaktikern schon immer warnend hingewiesen.
Wittmann und Müller
haben als Alternative zum streng formalen deduktiven Beweis das Konzept des „inhaltlich-anschaulichen
Beweises“ entwickelt und dazu ausgeführt: „Inhaltlich-anschauliche,
operative Beweise stützen sich dagegen auf Konstruktionen, von denen intuitiv
erkennbar ist, dass sie sich auf eine ganze Klasse von Beispielen anwenden
lassen und bestimmte Folgerungen nach sich ziehen.“[1]
Von Blum und Kirsch wurde zum „präformalen
Beweis“ weiterentwickelt, worunter sie „eine Kette von korrekten Schlüssen
verstehen, die auf nicht-formale Prämissen zurückgreifen.“[2]
Winter spricht von „Siehe-Beweisen“,
in denen sich „praktische Handlungen widerspiegeln“[3].
Für den Einsatz
von DGS wurde das zu „visuell-dynamischen
Beweisen“ weiterentwickelt, die (im Gegensatz zur reinen
Evidenz-Feststellung) eine Anwort auf die Frage ‚Warum ist das so?‘ geben
sollen.
„Sie sind
• visuell: anschaulich, auf eine Zeichnung bezogen als Figur, Eigenschaften und
Bezeichnung
• dynamisch: keine einzelne, starre Zeichnung, sondern eine ideale Zeichnung, eine
ganze Klasse von Figuren mit gleichen Eigenschaften, ermöglicht und sichtbar
gemacht durch den Zugmodus von DGS
• Beweis: ein vollgültiger Beweis in dem Sinne, dass er nicht durch rationale
Argumentationen zu erschüttern ist und in dem Sinne, dass eine Antwort auf die
Frage nach dem 'Warum' gegeben wird.“[4]
In der Folge der
Bilder, die im Zugmodus entstehen, kann ein Beweis als eine Geschichte in
Bildern[5]
aufgefasst werden. Das Arbeiten im Zugmodus hat so gewisse Verwandschaften mit
einem Trickfilm, der vor dem Auge (später auch vor dem geistigen Auge) abläuft.
Die lernpsychologisch entscheidenden
Unterschiede bestehen darin, dass bei DGS als interaktivem Medium
·
Schüler nicht passive Betrachter sind,
sondern aktiv Handelnde,
·
nicht mehr ein für alle gleicher Film abläuft,
sondern dass es individuelle Filme gibt, in denen Schüler selber Regisseure
sind,
·
der Zugmodus Möglichkeiten zum
experimentellen Arbeiten, zum Neuansatz bietet,
·
der Zugmodus Vermutungen produziert und
gleichzeitig eine Kontrollinstanz für diese Vermutungen bietet.
Die
vorgegebenen Konstruktionen sind dabei nicht als Einschränkungen der Möglichkeiten
für Schüler zu sehen; die mediale Brücke der elektronischen Arbeitsblätter
bietet über unsicherem Gelände den Schülern eine feste Ausgangsposition für
eigene Erkundungen.
Hierin
unterscheiden sie sich auch von manchen Java-Applets im Internet, in denen der
Schüler nur noch auf den Play-Knopf drücken kann, um eine trickfilmgleiche
Animation z. B. zum Beweis des Satzes von Pythagoras zu starten[6]
und somit wieder zum passiven Betrachter gemacht wird.
Im
Folgenden sollen nun einige Beispiele von elektronischen Arbeitsblättern[7]
vorgestellt werden. Die Aufgaben
orientieren sich zu großen Teilen am Standardstoff und bieten ihn in
dynamischer Form an. Hier gibt es viele klassische Ansätze, die mit DGS jetzt
einsichtiger und mit größerer Schüleraktivität unterrichtet werden können.
Für den Lehrer gibt es zusätzlich zu jeder Aufgabe eine schnelle Übersicht über
Lernziele, Lernvoraussetzungen und erwartete Lösung(en).
Um
Missverständnissen vorzubeugen, soll an dieser Stelle noch betont werden, dass
es nicht Ziel der elektronischen Arbeitsblätter ist, Geometrie-Unterricht
ausschließlich auf diese Weise zu betreiben. Handlungserfahrung (Schneiden,
Falten, Basteln, Herstellen beweglicher Modelle) ist wesentlich für den
internen Aufbau abstrakter Vorstellungen. Ebenso das händische Umgehen mit
Zirkel und Lineal, das auch im computergestützten Geometrie-Unterricht seine
Rolle behält, z.B. bei der Sicherung der Ergebnisse und bei Hausaufgaben, in
denen eine spezielle Figur aus der im Zugmodus erlebten Bilderfolge gezeichnet
wird.
In
den folgenden Beispiel-Aufgaben werden teils Schüler-Arbeitsblätter und teils
Lehrer-Informationen vorgestellt. Sie vermitteln auf dem Papier leider nur einen
ungenügenden Eindruck von den unterrichtlichen Chancen, die in ihnen stecken.

|
Lernziel: |
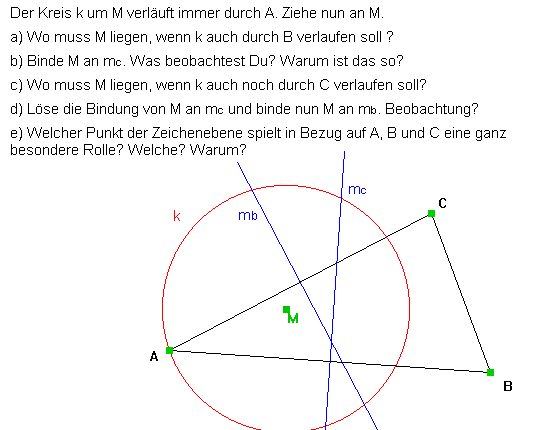
Die Schüler sollen einen Beweis des Umfangswinkelsatzes entdecken |
|
|
|
|
Voraussetzungen: |
Außenwinkelsatz bei Dreiecken, Thalessatz |
|
|
|
|
Euklid-Datei: |
A4-07.geo[9] |
|
|
|
|
|
|
|
|
|
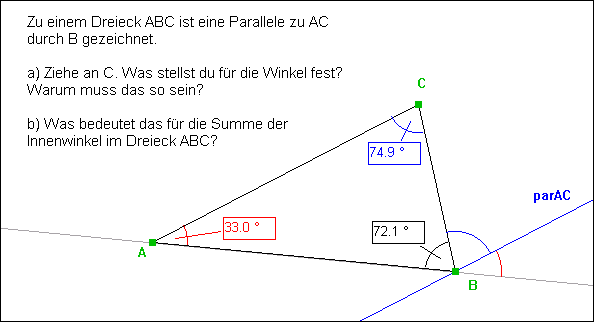
Arbeitsauftrag: |
Auf
einem Kreis um M liegen Punkte A, B, C. Sie bilden die Dreiecke ABC und
ABM. a)
Was stellst du für die markierten Teil-Winkel bei C und bei M fest? b)
Verändere die Dreiecke durch Ziehen an C (an A, B). Was
beobachtest Du? Warum muss das so sein? Tip: Betrachte das Dreieck AMC. c)
Was kann man entsprechend für die anderen Teil-Winkel bei C und M
aussagen? d) Der Mittelpunktswinkel bei M bleibt beim Bewegen von C konstant. Was folgt daraus für den Umfangswinkel bei C? |
|
|
|
|
Was dabei beobachtet werden kann: |
a) Der Teilwinkel bei M ist doppelt so groß wie der Teilwinkel bei C. b) Diese Eigenschaft bleibt beim Ziehen erhalten. Der gemessene Teil des Mittelpunktswinkels ist nach dem Außenwinkelsatz doppelt so groß wie der gemessene Teil des Umfangswinkels, da das Dreieck AMC gleichschenklig ist. c) Für die jeweiligen Restwinkel gilt das gleiche. d) Der Umfangswinkel an einem Kreisbogen ist konstant. |
|
|
|
|
Weitere Hinweise: |
Auch den Winkel MDA findet man als Außenwinkel
in doppelter Größe wieder bei Winkel CMA und Winkel BDM bei Winkel BMC. |
|
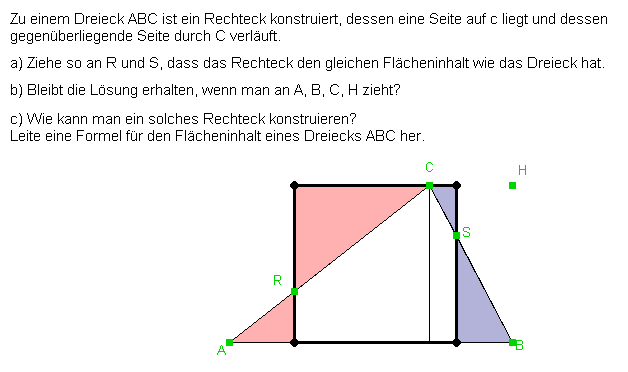
Lernziel: |
Die Schüler sollen die erste binomische Formel geometrisch entdecken. |
|
|
|
|
Voraussetzungen: |
Rechteckflächenberechnung |
|
|
|
|
Euklid-Datei: |
A7-01.geo |
|
|
|
|
|
|
|
|
|
|
Arbeitsauftrag: |
Ziehe an Zug-a und Zug-b. a) Wie groß ist die Fläche des gesamten Quadrates? b)
Aus welchen Teilflächen besteht das große Quadrat? Welche Gleichung
gilt somit offenbar? c)
Welche Gleichung gilt somit offenbar? |
|
|
|
|
Was dabei beobachtet werden kann: |
a) (a+b)2 b) a2, b2, ab, ba. c) Aus der Flächengleichheit folgt die erste binomische Formel: (a+b)2=a2+2ab+b2. |
|
|
|
Elektronische
Arbeitsblätter bieten eine Chance für den Geometrie-Unterricht,
Standard-Themen in moderner Form zu unterrichten.
Sie
ermöglichen dem normalen Lehrer im normalen Unterricht ohne
Spezialkenntnisse die Vorteile der DGS zu nutzen.
Sie
gehen auf die Erkenntnisse der Lernpsychologie ein.
Sie
ermöglichen selbsttätiges Lernen.
In
den nächsten Jahren wird sich in dieser Hinsicht viel bewegen.
Multimedia-Umgebungen und Internet werden diesen Prozess noch weiter
beschleunigen. Java-basierte Programme (z. B. Cinderella) werden erweiterte Möglichkeiten
für schülerorientierte Arbeitsblätter bieten.
Bender, Peter: Anschauliches Beweisen im
Geometrieunterricht - unter besonderer Berücksichtigung von (stetigen)
Bewegungen bzw. Verformungen. In: Kautschitsch/ Metzler: Anschauliches Beweisen.
Blum, Werner/
Kirsch Arnold: Warum haben nicht-triviale Lösungen von f ' = f
keine Nullstellen? Beobachtungen und Bemerkungen zum 'inhaltlich
anschaulichen' Beweisen. In: Kautschitsch/ Metzler: Anschauliches Beweisen.
Elschenbroich,
Hans-Jürgen: Geometrie beweglich mit Euklid. Dümmler, Bonn 1996.
Elschenbroich,
Hans-Jürgen: Dynamische Geometrieprogramme: Tod des Beweisens oder Entwicklung
einer neuen Beweiskultur? In: MNU 50/8, 1997.
Elschenbroich,
Hans-Jürgen: Visuelles Beweisen - Neue Möglichkeiten durch Dynamische
GeometrieSoftware. In: Beiträge zum Mathematikunterricht 1999. Vorträge auf
der 33. Tagung für Didaktik der Mathematik. Verlag franzbecker, Hildesheim,
Berlin 1999.
Elschenbroich,
Hans-Jürgen/ Seebach, Günther: Dynamisch Geometrie entdecken. Elektronische
Arbeitsblätter mit Euklid, Klasse 7/8. Dümmler-Stam, Köln 1999.
Holland, Gerhard:
Geometrie in der Sekundarstufe. Spektrum Akademischer Verlag.
Heidelberg 1996.
Hölzl, Reinhard:
Im Zugmodus der Cabri-Geometrie. Deutscher Studien Verlag. Weinheim 1994.
Kautschitsch, H./
Metzler, W. (Hrsg.): Anschauliches Beweisen. 7. und 8. Workshop zur
"Visualisierung in der Mathematik" in Klagenfurt im Juli 1987 und
1988. Hölder-Pichler-Tempsky, Wien 1989.
Winter, Heinrich:
Entdeckendes Lernen im Mathematikunterricht. Vieweg, Braunschweig 1991.
Wittmann, Erich
Christian; Müller, Gerhard: Wann ist ein Beweis ein Beweis? In:
Mathematikdidaktik: Theorie und Praxis. Festschrift für Heinrich Winter.
Cornelsen, Berlin 1988.
[1] Wittmann/ Müller, S. 249
[2] Blum/ Kirsch, S. 202f.
[3] Winter, S. 136f.
[4] Elschenbroich (1999) S. 159
[5] Hier muss darauf hingewiesen werden, dass dazu auch das Sehen geschult werden muss und dies ein Lernziel für sich ist! Es ist immer wieder zu beobachten, dass Schüler eine (für den Lehrer) bemerkenswerte Invarianz gar nicht beobachten, weil sie diese nicht sehen oder nicht für bemerkenswert halten. Das ist auch nicht verwunderlich, da die Schüler sowohl evolutionsgeschichtlich als auch als Kinder der Nintendo-Generation so geprägt sind, dass sie zunächst auf Veränderungen achten und nicht auf Invarianzen. Das Sehen im Zugmodus erfordert insofern zu guten Teilen eine Umkehrung der Sehgewohnheiten in Alltagssituationen.
[6] http://didaktik.physik.uni-wuerzburg.de/~pkrahmer/java/pythago/pythago.html
[7] Elschenbroich/ Seebach
[8] http://www.mathe-werkstatt.de/download.htm
[9] Die Bezeichnung der Dateien bezieht sich auf Elschenbroich/ Seebach.